|
|
|
$$V = \frac{A_{base} \times h}{3}$$
Volumen
$$A_{base} = \frac{3V}{h}$$
Área de base
$$h = \frac{3V}{A_{base}}$$
Altura
$$S_{tot} = A_{base} + S_{lat}$$
Área total
$$S_{lat} = S_{tot} - A_{base}$$
Superficie lateral
$$A_{base} = S_{tot} - S_{lat}$$
Área de base
Pirámide recta
$$S_{lat} = \frac{2p \times a}{2}$$
Superficie lateral
$$2p = \frac{2 \times S_{lat}}{a}$$
Perímetro de base
$$a = \frac{2 \times S_{lat}}{2p}$$
Apotema
$$r = \frac{2 \times A_{base}}{2p}$$
Radio inscrito
$$2p = \frac{2 \times A_{base}}{r}$$
Perímetro de base
$$A_{base} = \frac{2p \times r}{2}$$
Área de base
Usando el Teorema de Pitágoras
$$a = \sqrt{{h}^2 + {r}^2}$$
Apotema
$$r = \sqrt{{a}^2 - {h}^2}$$
Radio de base
$$h = \sqrt{{a}^2 - {r}^2}$$
Altura
Pirámide cuadrangular
$$A_{base} = {L}^2$$
Área de base
$$L = \sqrt{A_{base}}$$
Arista base
$$2p = L \times 4$$
Perímetro de base
$$L = \frac{2p}{4}$$
Arista base
$$r = \frac{L}{2}$$
Radio de base
$$L = 2 r$$
Arista base
Definición
Una pirámide es un poliedro formado por una cara poligonal, llamada base, y un punto externo a la base, llamado vértice.
Propiedad
- En una pirámide hay una cara base y caras laterales
- Las caras laterales de una pirámide son triángulos isósceles congruentes entre sí
- Altura: segmento perpendicular que conecta el vértice de la pirámide con el plano que contiene la base
- Apotema: en la pirámide regular, segmento que une el vértice con el punto medio de la arista base. Coincide con la altura de uno de los triángulos que forman las caras laterales
Otras definiciones
- Una pirámide recta es una pirámide en la que el polígono base está inscrito en una circunferencia y la altura une el vértice con el centro del círculo inscrito
- Una pirámide oblicua es cualquier pirámide que no sea recta
- Una pirámide regular es una pirámide que tiene un polígono regular como base
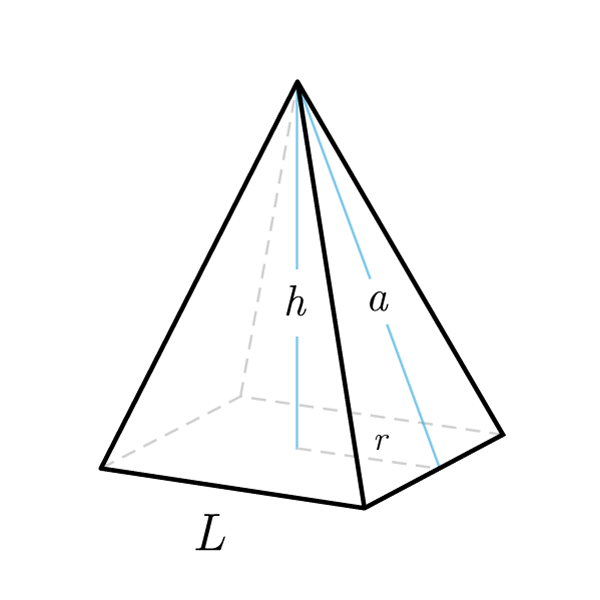
Fórmulas Pirámide
| Dado | Fórmula |
|---|---|
| Volumen | V = (Abase × h) / 3 |
| Área de base | Abase = (3V) / h |
| Altura | h = (3V) / Abase |
| Área total | Stot = Abase + Slat |
| Superficie lateral | Slat = Stot - Abase |
| Área de base | Abase = Stot - Stot |
Fórmulas Pirámide recta
| Dado | Fórmula |
|---|---|
| Superficie lateral | Stot = (2p × a) / 2 |
| Perímetro de base | 2p = (2 × Slat) / a |
| Apotema | a = (2 × Slat) / 2p |
| Radio inscrito | r = (2 × Abase) / 2p |
| Perímetro de base | 2p = (2 × Abase) / r |
| Área de base | Abase = (2p × r) / 2 |
| Apotema | a = √(h2 + r2) |
| Radio de base | r = √(a2 - h2) |
| Altura | h = √(a2 - r2) |
Fórmulas Pirámide cuadrangular
| Dado | Fórmula |
|---|---|
| Superficie lateral | Abase = L2 |
| Arista base | L = √(Abase) |
| Perímetro de base | 2p = L × 4 |
| Arista base | L = (2p) / 2 |
| Radio de base | r = L/2 |
| Arista base | L = 2r |