|
|
|
$$2p = L \times 4$$
Perímetro
$$L = \frac{2p}{4}$$
$$A = \frac{d_{1} \times d_{2}}{2}$$
Área
$$d_{1} = \frac{2A}{d_{2}}$$
Diagonal mayor
$$d_{2} = \frac{2A}{d_{1}}$$
Diagonal menor
$$L = \sqrt{ {\left(\frac{d_{1}}{2}\right)}^{2} + {\left(\frac{d_{2}}{2}\right)}^{2} }$$
Lado (Teorema de Pitágoras)
$$\frac{d_{1}}{2} = \sqrt{ {L}^{2} - {\left(\frac{d_{2}}{2}\right)}^{2} }$$
Semi-diagonal mayor
$$\frac{d_{2}}{2} = \sqrt{ {L}^{2} - {\left(\frac{d_{1}}{2}\right)}^{2} }$$
Semi-diagonal menor
Definición
Un rombo es un cuadrilátero con todos los lados congruentes.
Propiedad
- Cuatro lados congruentes, lados opuestos paralelos
- Ángulos congruentes opuestos, los ángulos consecutivos son suplementarios (su suma es 180°)
- Las diagonales son perpendiculares
- Las diagonales se encuentran en un punto llamado centro del rombo. El centro divide las diagonales en dos semidiagonales
- Las diagonales forman cuatro triángulos rectángulos congruentes, en los que la hipotenusa está representada por el lado del rombo y los catetos por las semidiagonales.
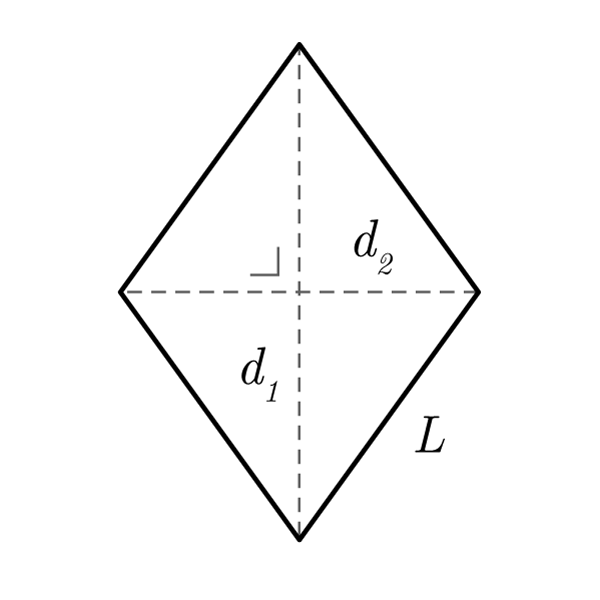
Fórmulas Rombo
| Dado | Fórmula |
|---|---|
| Perímetro | 2p = L× 4 |
| Área | A = (d1 × d2) / 2 |
| Lado | L = 2p / 4 |
| Lado | L = √[ (d1 / 2)2 + (d2 / 2)2 ] |
| Diagonal mayor | d1 = (2 × A) / d2 |
| Diagonal menor | d2 = (2 × A) / d1 |
| Semi-diagonal mayor | d1 / 2 = √[ L2 - (d2 / 2)2 ] |
| Semi-diagonal menor | d2 / 2 = √[ L2 - (d1 / 2)2 ] |