|
|
|
$$2p = B + b + L + h$$
Perímetro
$$A = \frac{\left(B + b \right) \times h}{2}$$
Área
$$B + b = \frac{2A}{h}$$
Suma de bases
$$h = \frac{2A}{B + b}$$
Altura
$$p_{1} = B - b$$
Proyección lado oblicuo
$$B - b = p_{1}$$
Diferencia base
$$B = b + p_{1}$$
$$b = B - p_{1}$$
Tr. Rectángulo formado por altura - lado oblicuo
$$L = \sqrt{ {p_{1}}^2 + {h}^2 }$$
Lado (Teorema de Pitágoras)
$$p_{1} = \sqrt{ {L}^2 - {h}^2 }$$
Proyección lado oblicuo
$$h = \sqrt{ {L}^2 - {p_{1}}^2 }$$
Altura
Tr. Rectángulo formado por altura - diagonal mayor
$$d_{1} = \sqrt{ {B}^2 + {h}^2 }$$
Diagonal mayor (Teorema de Pitágoras)
$$B = \sqrt{ {d_{1}}^2 - {h}^2 }$$
Base principal
$$h = \sqrt{ {d_{1}}^2 - {B}^2 }$$
Altura
Tr. Rectángulo formado por altura - diagonal menor
$$d_{2} = \sqrt{ {b}^2 + {h}^2 }$$
Diagonal menor (Teorema de Pitágoras)
$$b = \sqrt{ {d_{2}}^2 - {h}^2 }$$
Base menor
$$h = \sqrt{ {d_{2}}^2 - {b}^2 }$$
Altura
Definición
Un trapezoide en ángulo recto es un trapezoide con un ángulo recto (90 grados).
Propiedad
- Tiene un ángulo recto (90 grados)
- Se aplican todas las fórmulas del Trapecio genérico
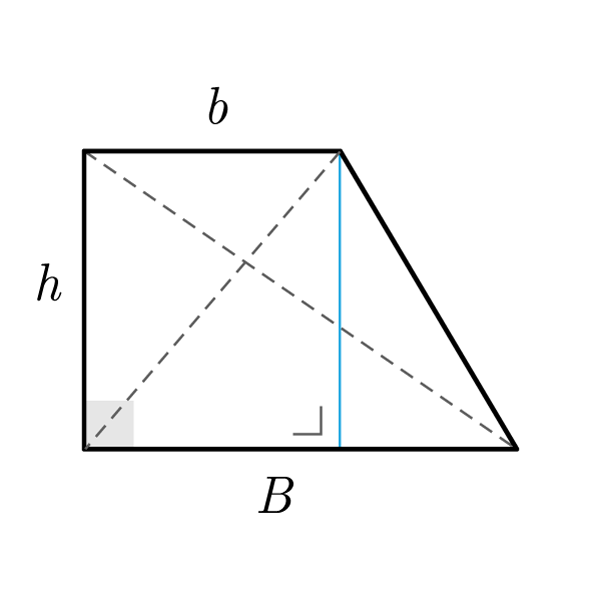
Fórmulas Trapecio rectángulo
| Dado | Fórmula |
|---|---|
| Perímetro | 2p = B + b + L + h |
| Área | A = [(B + b) × h] / 2 |
| Altura | h = (2 × A) / (B + b) |
| Proyección lado oblicuo | p1 = B - b |
| Suma de bases | B + b = (2 × A) / h |
| Suma de bases | B + b = 2p - 2 × L |