|
|
|
$$2p = b + L \times 2$$
Perímetro
$$b = 2p - L \times 2$$
$$L = \frac{2p - b}{2}$$
$$A = \frac{b \times h}{2}$$
Área
$$b = \frac{A \times 2}{h}$$
$$h = \frac{A \times 2}{b}$$
$$L = \sqrt{ {h}^2 + {\left(\dfrac{b}{2}\right)}^2 }$$
Lado oblicuo (Teorema de Pitágoras)
$$h = \sqrt{ {L}^2 - {\left(\dfrac{b}{2}\right)}^2 }$$
$$b = \sqrt{ {L}^2 - {h}^2 } \times 2$$
Definición
Un triángulo isósceles es un triángulo con dos lados congruentes.
Propiedad
- Dos lados congruentes
- Ángulos en la base congruentes
- Se aplican todas las fórmulas del Triángulo genérico
- La altura relativa a la base la divide en dos triángulos rectángulos congruentes. Para estos se aplican las fórmulas del Triángulo rectángulo
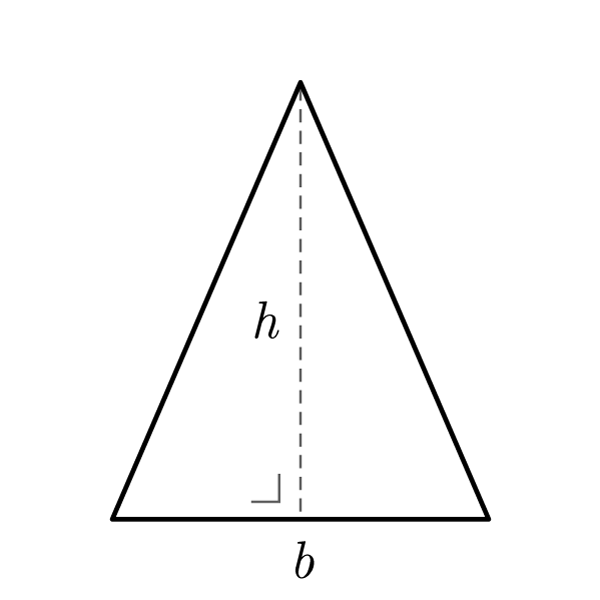
Fórmulas Triángulo isósceles
| Dado | Fórmula |
|---|---|
| Perímetro | 2p = b + L × 2 |
| Área | A = (b × h) / 2 |
| Lado oblicuo | L = √[ h2 + (b / 2)2 ] |
| Base | b = (A × 2) / h |
| Altura | h = (A × 2) / b |
| Base | b = 2p - L × 2 |
| Lado | L = (2p - b) / 2 |
| Altura | h = √[ L2 - (b / 2)2 ] |
| Base | b = √( L2 - h2 ) × 2 |