|
|
|
$$V = \frac{\pi {r}^{2} h}{3}$$
Volumen
$$r = \sqrt{\frac{3 V}{\pi h}}$$
Radio
$$h = \frac{3 V}{\pi {r}^{2}}$$
Altura
$$V = \frac{A_{base} h}{3}$$
Volumen
Usando el Teorema de Pitágoras
$$a = \sqrt{{h}^2 + {r}^2}$$
Apotema
$$h = \sqrt{{a}^2 - {r}^2}$$
Altura
$$r = \sqrt{{a}^2 - {h}^2}$$
Radio
Superficie lateral
$$S_{tot} = A_{base} + S_{lat}$$
Área total
$$S_{lat} = S_{tot} - A_{base}$$
Superficie lateral
$$S_{lat} = \pi r a$$
Superficie lateral
$$r = \frac{S_{lat}}{\pi a}$$
Radio
$$r = \frac{S_{lat}}{\pi r}$$
Apotema
$$A_{base} = \pi {r}^2$$
Área de base
$$A_{base} = S_{tot} - S_{lat}$$
Área de base
Otras fórmulas
$$2 r = a$$
Cono equilátero
Definición
Un cono es un sólido de rotación que se obtiene rotando un triángulo rectángulo alrededor de uno de sus catetos.
Propiedad
- En un cono - el radio, la altura y la apotema forman un triángulo rectángulo
- Un cono es equivalente (tiene el mismo volumen) a un tercio de un cilindro con un radio y una altura de la misma longitud que los del cono
- Un cono equilátero es un cono en el que el diámetro y la apotema tienen la misma longitud
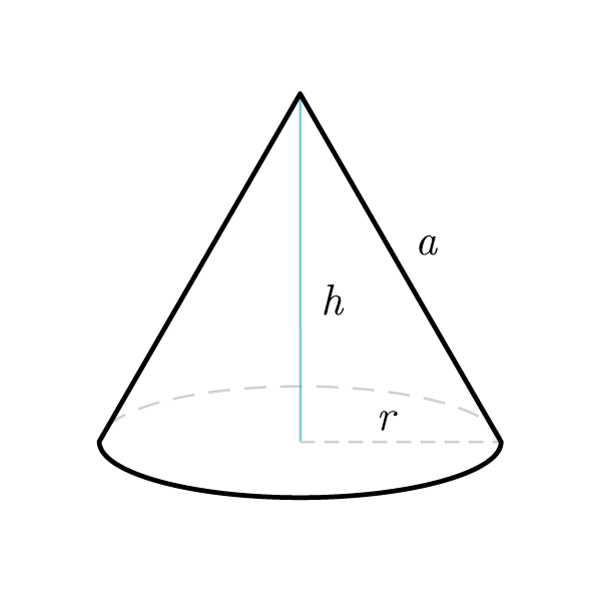
Fórmulas Cono
| Dado | Fórmula |
|---|---|
| Volumen | V = (π r2 h) / 3 |
| Radio | V = √[ (3V) / (π h) ] |
| Altura | h = (3V) / (π r2) |
| Volumen | V = (Abase × h) / 3 |
| Apotema | a = √(h2 + r2) |
| Altura | h = √(a2 - r2) |
| Radio | r = √(a2 - h2) |
| Área total | Stot = Abase + Slat |
| Superficie lateral | Slat = Stot - Abase |
| Superficie lateral | Slat = π r a |
| Radio | r = Slat / (π a) |
| Apotema | a = Slat / (π r) |
| Área de base | Abase = π r2 |
| Área de base | Abase = Stot - Slat |