|
|
|
$$2p = 2a+2b$$
Perímetro
$$A = a \times b$$
Área
$$a = \frac{A}{b}$$
Dimensión mayor
$$b = \frac{A}{a}$$
Dimensión menor
$$d = \sqrt{{a}^{2} + {b}^{2}}$$
Diagonal (Teorema de Pitágoras)
$$a = \sqrt{{d}^{2} - {b}^{2}}$$
Dimensión mayor
$$b = \sqrt{{d}^{2} - {a}^{2}}$$
Dimensión menor
Definición
Un rectángulo es un cuadrilátero con ángulos internos congruentes (todos rectos) y lados opuestos congruentes.
Propiedad
- Los lados se llaman dimensiones, con uno mayor y otro menor. Las dimensiones opuestas son congruentes (los lados son congruentes de dos en dos)
- Los lados también pueden denominarse base (dimensión mayor) y altura (dimensión menor), o también largo (dimensión mayor) y ancho (dimensión menor)
- Cuatro ángulos rectos congruentes
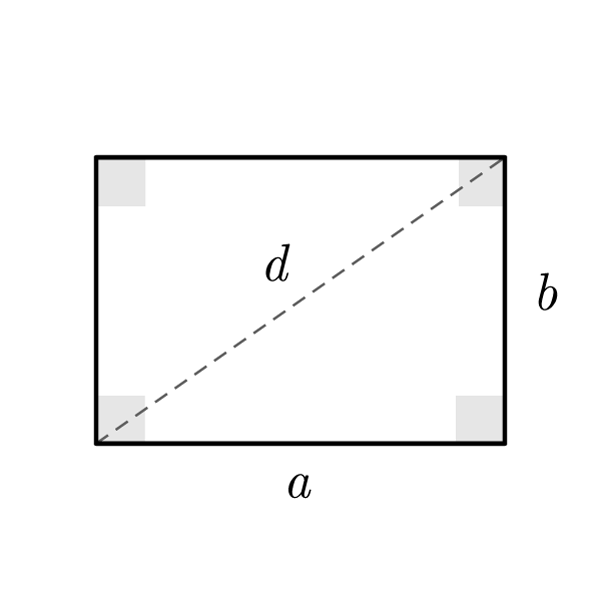
Fórmulas Rectángulo
| Dado | Fórmula |
|---|---|
| Perímetro | 2p = 2 × a + 2 × b |
| Área | A = a × b |
| Diagonal | d = √( a2 + b2 ) |
| Dimensión mayor | a = A / b |
| Dimensión menor | b = A / a |
| Dimensión mayor | a = √( d2 - b2 ) |
| Dimensión menor | b = √( d2 - a2 ) |